INTRODUCTION
One key limiter of the speed of our robot so far is the time of flight sensors. At higher speeds, the sensors can't update fast enough to keep up with the changes. To fix this, I'll take a step away from deterministic robotics and embrace the probabilistic world we live in. Through many informative lectures, I've learned that one of the best ways to make problamatic sensors better is to implement a Kalman Filter. This filter takes a model determined and derived from simple dynamics, and averages this model against the numbers I'll gather from my sensors. This means the bot is about to infer its distance even when it can't read its sensors. To do this, I'll be following the helpful instructions found in lab 7.
INITIAL CONDITIONS
In order to build our model, we need to estimate just how much inertia the bot has and how much drag forces it experiences (friction included). To do this, I run my bot at about 80% speed toward the wall and stop just before hitting it. Below are the gathered graphs.
Left: Raw distance data collected by sensors as fast as possible.
Middle: Extrapolated distance and speed.
Right: Input motor power as a percentage of total power.
Using the above equations and the data gathered, the mass and drag force of the system can be determined and we can build the system's state space.
Assuming the final value of speed is approximately steady state, I can determine that the 90% rise time
happens at approximately .898 seconds,
meaning that:
Drag = 0.451 N
Mass = 0.176 Kg
The state space equation for this system is as follows:
where A, B, and x are
KALMAN FILTER SANITY CHECK
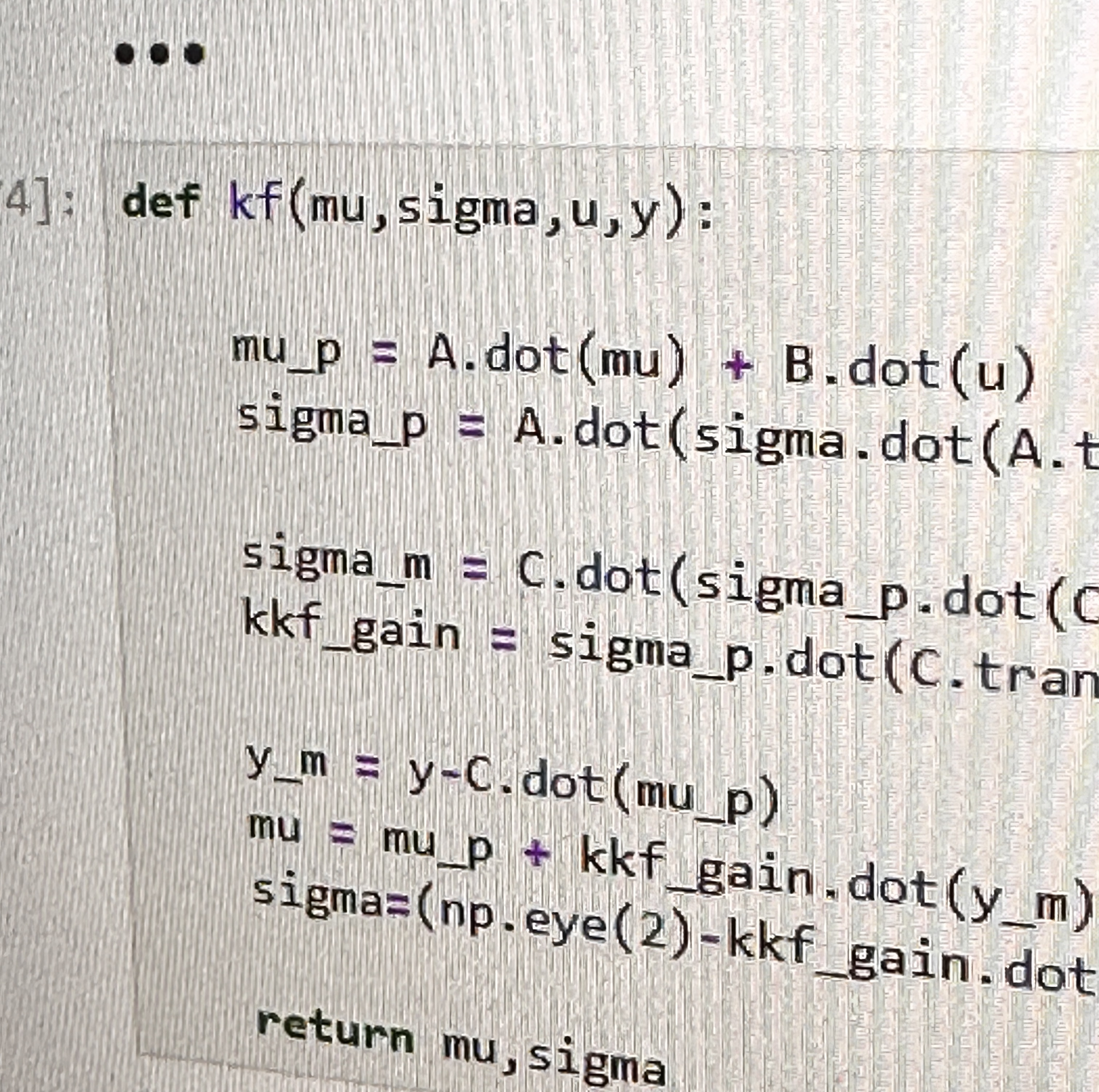
The Kalman filter works by updating a state, x, that contains estimates of the current position x[0] and speed x[1] and a sigma that holds the current uncertainty. To start, I need to initialize some starting uncertainty on each value in the state. To test that I did the right algorithm I can run the Kalman Filter on any distance data that I've collected so far. Below is the same distance data with kalman filter estimates overlayed on it (dots are the values that the bot would see) followed by the code used.
The uncertainties used as the basis of the estimate can also be seen in the code. Changing these uncertainties mean the Kalman filter will weight inputs differently. Increasing sigma 1 or 2 results in this (σ1 = 100 σ2 = 100 σ3 = 1).
By making the model uncertainties so high, we're essentially saying there is a high probability that the model we made is inaccurate. By doing so, the filter trusts the sensor readings the most. This can be bad at the first and last time steps where the model could be best used to interpolate points. By increasing sigma 3 we see the following. (σ3 = 100 σ1 = 1 σ2 = 1)
The Kalman Filter now distrusts the sensor readings. After receiving a lot of sensor readings, the model will eventually adjust itself, however, focusing on our model will cause the filter to lag behind the sensor quite a bit.
IMPLEMENTATION
So far, all this implementation had been done on jupyter labs with previously collected sensor data and plenty of aid from Professor Kirsten, Anya Prabowo, Jonathan Jaramillo, and helpful tips from students. In order to make use of this algorithm, I had to implement it myself on the robot through Arduino. Luckilly for me, I've taken note that the filter itself is pretty robust. It can correct for most inaccuracies I might give it.
The above left is the result of the Kalman Filter in action on the stunt from lab 6. The Kalman filter does a fairly good job of interpolating data points between time of flight readings coming up to the wall (closer look on the right) and afterwards the model struggles to keep up with the random readings invoked by turning around. Below is a video showing just that.
CONCLUSION
The Kalman filter is an excellent tool for fusing sensors with reality. Being able to use models from system dynamics to correct noisy sensor data has been my favorite subject-crossover ever and after implementing the algorithm myself on the arduino, I'm confident its implementation will benefit the robot.